What Does the Sigma Symbol Mean in Statistics? Deviation!
In statistics, the sigma symbol (σ) represents the standard deviation of a dataset, which measures the dispersion or variability of the data points around the mean value.
The sigma symbol, denoted as σ, is derived from the Greek letter ‘sigma’ and is used in various mathematical and statistical concepts. In statistics, it specifically represents the standard deviation.
Standard deviation quantifies the degree of variation or dispersion in a dataset. In simpler terms, it tells us how spread out the data points are from the mean value and indicates the consistency or uniformity of the data.
Standard deviation plays a significant role in various statistical analyses, as it helps determine the reliability and consistency of the data being analyzed.
Being able to calculate and understand standard deviation allows researchers to gain insights into the patterns and trends within the data, ultimately leading to more accurate predictions and conclusions.
Understanding the Sigma Symbol in Statistics
| Sigma Symbol (Σ) | Meaning in Statistics |
|---|---|
| Definition | The Sigma symbol (Σ) is a Greek letter used to represent the sum of a set of values or quantities in statistics. It is called the summation operator. |
| Usage | Σ is used when dealing with multiple values to compute various statistical measures such as mean, variance, and standard deviation. |
| Formula | For a given sequence, xi, and a range of values from i=1 to n, the summation is written as: Σ(xi) for i=1 to n. |
| Example | If we have the values 2, 4, and 6, we can write their sum using the Sigma symbol as: Σ(xi) for i=1 to 3 = 2 + 4 + 6 = 12. |
Key Takeaway
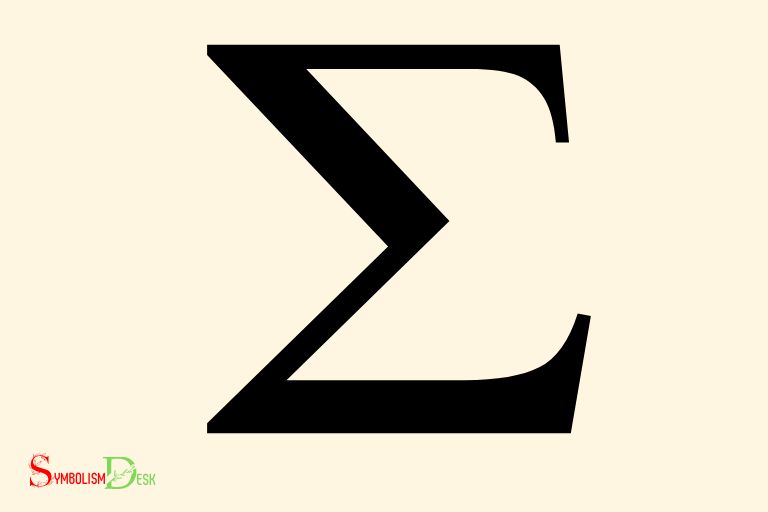
Five Facts About: The Sigma Symbol in Statistics
What Is The Sigma Symbol?
The sigma symbol is a statistical term utilized to symbolize a population’s standard deviation. It is a greek letter and is represented by the symbol ‘σ’.
The sigma symbol has played a critical role in statistical analysis, and it’s a vital element in diverse statistical calculations.
In this blog post, we will discuss in detail what the sigma symbol is, its definition, how it’s used, and its importance in statistical calculations.
Definition And Meaning Of The Sigma Symbol In Statistical Analysis
The sigma symbol denotes standard deviation and is widely utilized in statistical computation to determine the amount of variability in data. In more precise scientific terms, it refers to the average dispersion from the mean.
Some crucial points to note about the sigma symbol’s definition are as follows:
- The sigma symbol, ‘σ’, is a greek letter that represents standard deviation in statistics.
- The sigma symbol’s primary aim is to determine the degree of variation in a given set of numerical data.
- The formula for calculating sigma depends on the size of the dataset and the type of distribution.
Importance Of The Sigma Symbol In Statistical Calculations
The sigma symbol is essential in statistical analysis and carries significance in the calculation of statistical observations.
Here are the key points to note about the importance of the sigma symbol in statistical calculations:
- The sigma symbol helps in determining the degree of data variability and spread in various dispersion measures like variance, coefficient of variation, etc.
- Sigma plays a crucial role in the formulation of the central limit theorem, a statistical concept that describes the distribution of data samples.
- The sigma symbol is a crucial component in statistical hypothesis testing. In hypothesis testing, sigma is often utilized to form the null hypothesis used in statistical tests.
How The Symbol Is Used In Representing Standard Deviation
The sigma symbol is used widely in representing standard deviation, which aids in describing the amount of variability or spread in a given dataset.
Here are the key points worth noting:
- Sigma symbol indicates standard deviation in a data sample, where the sigma notation denotes the formula’s summation.
- The sigma symbol also represents population standard deviation, which measures how much variability there is among all possible data points in a population.
- The sigma symbol is often replaced by ‘s’ to represent sample standard deviation. The formula for sample standard deviation uses n-1 in the denominator instead of n, where n is the total number of observations.
The sigma symbol is a crucial statistical concept that plays a vital role in data analysis. It is utilized to determine a population’s standard deviation, measure data variability, and has significant importance in statistical calculations.
By understanding the sigma symbol’s meaning and applications, researchers and statisticians can accurately obtain valuable insights and conclusions from collected datasets.
Types Of Sigma Symbols
Explanation Of The Different Types Of Sigma Symbols And Their Uses In Statistical Analysis
In statistics, sigma symbol (σ) is used to represent standard deviation. Standard deviation denotes the amount of variation or dispersion of a set of data from the mean. There are different types of sigma symbols used in statistical analysis to represent different things.
Here are some of the different types:
- Population standard deviation symbol (σ): This is the most common sigma symbol used in statistical analysis. It represents the standard deviation of a population.
- Sample standard deviation symbol (s): This symbol is used to represent the standard deviation of a sample. In statistics, a population is a group of all items of interest, while a sample is a smaller group selected from the population.
- Lowercase σ symbol: This symbol is used to denote the standard deviation of a population, while the lowercase s symbol represents the standard deviation of a sample.
Difference Between Uppercase And Lowercase Sigma Symbols
In statistical analysis, the upper and lowercase sigma symbols have different meanings. The uppercase sigma (σ) is used to denote the sum of a set of numbers, while the lowercase sigma (σ) represents standard deviation.
Here are some key differences between the uppercase and lowercase sigma symbols:
- Uppercase sigma (σ): This symbol is used to represent the sum of a series of numbers. It is often used with an index i in the lower part of the symbol. For example, σi=1^5 i represents the sum of the numbers 1 through 5, which is 15.
- Lowercase sigma (σ): On the other hand, this symbol denotes standard deviation in statistical analysis. It is used to determine the amount of dispersion or variation of a set of data in relation to the mean.
How To Choose The Right Type Of Sigma Symbol Depending On The Scenario
Choosing the right type of sigma symbol can be confusing, especially for beginners.
Here are some tips to help you choose the right type of sigma symbol depending on the scenario:
- Use the uppercase sigma symbol (σ) when you want to represent the sum of a series of numbers
- Use the lowercase sigma symbol (σ) to denote the standard deviation of a set of data.
- If you are working with a population dataset, use the population standard deviation symbol (σ).
- On the other hand, if you are working with a sample dataset, use the sample standard deviation symbol (s).
In statistical analysis, using the right type of sigma symbol is crucial for accurate results. Therefore, it is essential to understand the different types and their uses.
How To Use The Sigma Symbol In Statistical Calculations
Understanding The Sigma Symbol In Statistical Calculations
The sigma symbol (σ) is an important statistical tool that is used to indicate the standard deviation or variability of a data set. It is a greek letter that is commonly used in different fields of study, including mathematics, physics, and engineering.
In statistics, the sigma symbol is used to represent the standard deviation of a population, and it is also used to indicate the sum of a series of numbers.
We will explore how to use the sigma symbol in statistical calculations, examples of sigma symbol calculations in real-life scenarios, common mistakes, and pitfalls to avoid when using the sigma symbol in statistical calculations.
Step-By-Step Guide On How To Compute For Standard Deviation Using The Sigma Symbol
The standard deviation is a measure of the amount of variation or dispersion in a set of data values. It is an important concept in statistics and is used to help understand the distribution of data.
The following are the steps to calculate standard deviation using the sigma symbol:
- Calculate the mean (average) of the data set
- Find the difference between each data point and the mean
- Square the differences
- Add up the squares of the differences
- Divide the sum of the squares of the differences by the number of data points minus one
- Take the square root of the resulting value to obtain the standard deviation.
The formula for standard deviation using the sigma symbol is:
`Σ = Sqrt[Σ(X-Μ)²/N-1]`
Where σ is the standard deviation, x is the data value, μ is the mean of the data set, σ represents the sum, and n is the number of data points.
Examples Of Sigma Symbol Calculations In Real-Life Scenarios
The sigma symbol is used widely in many different fields, including science, engineering, and finance.
Here are some examples of sigma symbol calculations in real-life scenarios:
- In manufacturing, the sigma symbol is used to represent the number of standard deviations that a process is from the mean. A process with six standard deviations from the mean has a value of σ = 6. This is used to indicate how far a process is from the ideal performance state.
- In physics, the sigma symbol is used to represent the cross-section of a nucleus in atomic and nuclear physics. It is also used to represent standard deviation in measurements of radiation dose and energy.
- In finance, the sigma symbol is used to represent the volatility of a stock or market. A high value of sigma indicates a high level of volatility, while a low value indicates low volatility.
Common Mistakes And Pitfalls To Avoid When Using The Sigma Symbol In Statistical Calculations
Using the sigma symbol in statistical calculations can be challenging for beginners, and it is important to avoid common mistakes and pitfalls.
Here are some tips to help you avoid these:
- Make sure to use the correct formula for standard deviation, and be careful with parentheses and brackets.
- Always double-check your work to ensure that you have not made any mistakes while entering or calculating the data.
- Be cautious when dealing with large data sets, as they can lead to computational errors. Break them down into smaller groups before making any calculations.
- Do not forget to consider the context of the problem, and do not simply rely on formulas and calculations.
- Be cautious when interpreting the sigma symbol in different contexts, as it can mean different things in different fields of study.
The sigma symbol is an essential tool in statistical calculations that is used to represent standard deviation and the sum of a series of numbers.
Understanding how to use it correctly and avoiding common mistakes and pitfalls can help you make accurate calculations and more informed decisions.
The Significance Of The Sigma Symbol In Research And Data Analysis
Discussion Of How The Sigma Symbol Impacts Research And Data Analysis
In statistical analysis, the sigma symbol (σ) represents the standard deviation of a given dataset, which is a measure of the amount of variation or dispersion around the mean.
Understanding the significance of the sigma symbol is crucial for conducting accurate research and data analysis.
Here are some of the ways this impacts the process:
- Large standard deviations indicate that the data points are widely spread out, whereas small standard deviations indicate that the data points are clustered around the mean. This information helps researchers make informed decisions about how to collect, analyze, and present data.
- The sigma symbol is used widely in statistical hypothesis testing, which involves determining whether a given hypothesis about a population parameter is supported by the data. Standard deviation plays a crucial role in this process.
- The sigma symbol is also an essential component of the normal distribution, which is a common probability distribution used in statistical analysis. Working with the sigma symbol helps researchers better understand the shape and characteristics of a normal distribution, leading to more accurate data analysis.
Importance Of Understanding The Sigma Symbol In Improving Data Accuracy
The sigma symbol is a vital tool for ensuring the accuracy of statistical data analysis.
Here are some of the reasons why:
- When working with a dataset that has a large standard deviation, there is more variability among the data points. To avoid inaccuracies in findings, researchers must correctly account for this variation.
- The sigma symbol helps researchers identify patterns and trends in a dataset, which can be used to make predictions about future observations.
- By knowing the sigma symbol’s interpretation, researchers can communicate more effectively with stakeholders, including colleagues, clients, and sponsors.
Explanation Of How The Sigma Symbol Helps In Identifying Outliers And Anomalies In Data Analysis
The sigma symbol plays an essential role in identifying outliers and anomalies in statistical data analysis.
Here’s why:
- Using the sigma symbol, researchers can define the range or limits within which the data is considered normal or expected. Outliers and anomalies beyond this range help identify unexpected results or problems with the data.
- The sigma symbol can also help to identify trends or patterns that are different from the expected value, again indicating a need for further investigation of the data.
- By identifying outliers and anomalies using the sigma symbol, researchers can ensure that their conclusions are based on accurate data and do not distort the results.
Does the Symbol “&” Have a Different Meaning in Statistics Compared to its Conjunction Meaning?
In statistics, the symbol & has a different symbol meaning conjunction and compared to its usual conjunction meaning. Within statistics, the & symbol is often used to represent the logical operator and when combining criteria or conditions. This particular use of the symbol distinguishes it from its conventional meaning as a conjunction.
FAQ The Sigma Symbol Mean In Statistics
What Does The Sigma Symbol Mean In Statistics?
In statistics, the sigma symbol represents the standard deviation of a population or a sample.
How Is The Sigma Symbol Used In Statistics?
The sigma symbol is used to measure the variability of a set of numerical data.
What Is The Difference Between Sigma And Mu In Statistics?
Sigma represents the standard deviation, while mu represents the mean or average of a set of data.
Why Is The Sigma Symbol Important In Statistics?
The sigma symbol is important in statistics because it can help us understand how much the data varies from the mean.
How Do You Calculate Sigma In Statistics?
To calculate sigma in statistics, you need to find the square root of the variance, which is the average of the squared differences from the mean.
Conclusion
The sigma symbol is a statistical symbol used to represent standard deviation, which is a measure of the amount of variation or dispersion of a set of data values.
By understanding the sigma symbol and its meaning, you can better interpret and analyze statistical data.
In this article, we have covered the use and meaning of the sigma symbol in statistics, as well as how to calculate it, its relationship with normal distribution, and its significance in quality control.
Whether you are a student of statistics or a working professional, understanding the sigma symbol is a critical aspect of data analysis and decision-making.
With this knowledge, you can efficiently interpret statistical data and make more well-informed decisions.
Therefore, mastering the use of the sigma symbol can help you to succeed in your career and understand the world around you more accurately.







